얼마전 채권평가사 중 한 곳에서 c++을 이용하여 엔진을 개발했다고 한다. 기존의 c엔진보다 속도나 유연성, 확장성을 높이기 위해서라고 그 이유를 밝혔었는데 언어의 확장성은 사실 중요한 요소이긴 하다. 특히 금융상품들을 분석하다보면 비슷한 패턴의 속성(예를들면 cashflow를 이용한 할인법이나 이자율 추정 방법 등)들이 반복되므로 c++언어 자체의 상속성과 캡슐화 등이 유용할 수 있다. 특히 이미 잘 짜여진 c++의 템플릿을 통한 연산속도의 향상은 반복계산시 어느정도 성능차이를 불러올 수도 있다.
그러나, 언어 자체의 차이도 중요하지만 언어를 잘 사용하는 것도 아주 중요한 요소 중 하나이다. c++와 c 둘 중에서 어느 쪽에 더 낫다라고 말하기는 애매한 상황이라서 아무래도 개발이 쉬운 c를 선택했다(언젠가 java로도 포팅해 볼 예정이다).
채권 가격 계산을 위해 제일 먼저 덤벼든 부분은 일반채권(SB : straight bond)이다. 일반 채권 중에서도 이표채(Coupon Bond)를 먼저 소개한다. 여기서는 채권의 기본인 가격 계산과 duration, convexity를 함께 계산할 수 있도록 작성을 했다. 채권수익률은 ytm 하나를 사용할 수도 있고 spot rate를 사용할 수도 있다.
가격 계산에서의 YTM과 SPOT
YTM(Yield to Maturity)은 일반적으로 만기까지의 수익률로 이해할 수 있지만 가격 계산적인 측면에서 볼 때는 만기에 따라 서로 다른 spot rate을 다 적용안 것과 동일한 역할을 하는 하나의 수익률이다.
즉, 1M -> 3.45, 3M -> 3.47, 6M -> 3.49, 9M -> 3.50와 같이 서로 다른 spot rate(할인율)을 적용해서 계산해야 하는데 그냥 3.48로 계산했을 때 동일한 결과가 나오게 해 주는 수익률이 YTM이다.
다음은 아직 미결사항이 조금 남아 있는 소스이다. 선매출과 경과이자에 대한 계산은 포함하지 않는다.
/*-----------------------------------------------------------------------------
* bond_sb.c
* : SB ( Straight Bond )를 계산하기 위한 함수
* 가격계산시 duration, convexity를 계산함
*
*---------------------------------------------------------------------------*/
#ifndef _BOND_SB_C_
#define _BOND_SB_C_
#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include "define.h"
#include "util.h"
#include "bond_lib.h"
#include "math_util.h"
#include "date_lib.h"
/*-----------------------------------------------------------------------------
* fnSBCouponBond : 이표채에 대한 가격 계산 함수
* Spot/YTM 모두 사용가능
* YTM의 갯수를 1개만 지정하는 경우 해당 YTM을 사용할 수 있으며,
* YTM의 갯수가 여러개인 경우 보간 하여 해당 YTM 사용
*
* 미결사항 :
*---------------------------------------------------------------------------*/
UINT fnSBCouponBond( DATETYPE dtPriceDay, /* 계산일 */
BONDINFO *pBondInfo, /* Bond Info Structure */
CURVE *pCurve, /* ytm/sport curve */
BONDPRICE *pBondPrice, /* Price Info Structure */
INT *error_code )
{
DATETYPE nextCouponDate;
DATETYPE prevCouponDate;
DATETYPE nextDate;
DATETYPE prevDate;
DATETYPE dtBaseDate;
CASHFACTOR *pCashFactor;
UINT nTotalCoupon;
DOUBLE nCashIn;
DOUBLE nDuration;
DOUBLE nMD;
DOUBLE nConvexity;
DOUBLE nBondPrice;
DOUBLE nInterest;
DOUBLE nFace;
DOUBLE nDiscountToday;
UINT nIntPayType;
UINT nCouponPerYear;
UINT nNextCouponRemDay;
UINT nCouponTermDay;
int idx;
int nCouponIdx;
...
중략
...
//초기화
nFace = 10000.0;
nCouponPerYear = 12.0 / pBondInfo->nIntMonth;
nInterest = nFace * pBondInfo->nCouponRate / nCouponPerYear;
nFace = nFace * pBondInfo->nReturnRate / 100.0;
nTotalCoupon = fnCountDate( dtPriceDay, pBondInfo->dtDueDay, MONTH ) / pBondInfo->nIntMonth + 3;
...
// 만기가 지나거나 발행정보가 잘못되었는지 체크하고 잘못되었을땐 리턴하도록 하는 부분 포함
...
//
// 이자를 지급하는 기준이 발행일 말일 기준인지, 만기일 말일 기준인지, 발행일 기준인지, 만기일 기준인지를 판단한다.
pCashFactor = (CASHFACTOR*)calloc( nTotalCoupon, sizeof( CASHFACTOR ) );
nIntPayType = pBondInfo->nIntPayType;
if ( nIntPayType == ENGINE_SELECT ) {
if ( fnIsDate( pBondInfo->dtFirstIntDay ) && fnIsLastDay( pBondInfo->dtFirstIntDay ) && pBondInfo->bEndOfMonth )
nIntPayType = ISSUE_MONTH_LAST_DAY;
else if ( fnIsDate( pBondInfo->dtFirstIntDay ) &&
fnDatetoInt( pBondInfo->dtFirstIntDay ) == fnDatetoInt( fnAddDateInt( pBondInfo->dtIssueDay, MONTH, pBondInfo->nIntMonth ) ) )
nIntPayType = ISSUE_DAY;
else if ( fnIsDate( pBondInfo->dtFirstIntDay ) )
nIntPayType = IRREGULAR_FIRST;
else if ( fnIsDate( pBondInfo->dtLastIntDay ) && fnIsLastDay( pBondInfo->dtLastIntDay ) )
nIntPayType = MATURE_MONTH_LAST_DAY;
else if ( fnIsDate( pBondInfo->dtLastIntDay ) &&
fnDatetoInt( pBondInfo->dtLastIntDay ) == fnDatetoInt( fnAddDateInt( pBondInfo->dtLastIntDay, MONTH, -pBondInfo->nIntMonth ) ) )
nIntPayType = MATURITY_DAY;
else if ( !fnIsDate( pBondInfo->dtFirstIntDay ) && !fnIsDate( pBondInfo->dtLastIntDay ) ) {
if ( fnIsLastDay( pBondInfo->dtIssueDay ) && pBondInfo->bEndOfMonth )
nIntPayType = ISSUE_MONTH_LAST_DAY;
else
nIntPayType = ISSUE_DAY;
}
else if ( fnIsDate( pBondInfo->dtLastIntDay ) )
nIntPayType = IRREGULAR_LAST;
}
/* 발행일 기준 이자지급 채권 */
if ( nIntPayType == ISSUE_DAY || nIntPayType == IRREGULAR_FIRST ) {
if ( nIntPayType == ISSUE_DAY )
// 가격 계산일이 발행일보다 이전인 경우(발행도 안된 채권을 사는 것이다!)
if ( fnDatetoInt( pBondInfo->dtIssueDay ) > fnDatetoInt( dtPriceDay ) ) {
prevCouponDate = dtPriceDay;
// 다음 이자지급일은 발행일에 이자지급 주기를 그냥 더한다.
nextCouponDate = fnAddDateInt( pBondInfo->dtIssueDay, MONTH, pBondInfo->nIntMonth );
}
// 이미 발행된 채권이라면 다음 이자지급일은 발행일을 기점으로 더해나가야 한다.
// (단 prevCouponDate == nextCoupondate를 해 놓고 아래에서 loop 돌면서 찾는다.)
else {
nextCouponDate = pBondInfo->dtIssueDay;
prevCouponDate = nextCouponDate;
}
else {
nextCouponDate = pBondInfo->dtFirstIntDay;
prevCouponDate = nextCouponDate;
}
dtBaseDate = nextCouponDate;
// 가격 계산일이 다음 이자지급일 직전 구간에 오도록 날짜를 더해간다
// 사실 간단한 로직으로 한번에 구할 수도 있다.( 발행일 + floor((가격계산일 - 발행일 ) / 이자지급주기 ) * 이자지급주기 ) 그러나 프로그램을 Copy and paste 쉽게 하기 위해 풀어썼다. ^^;;
while ( fnDatetoInt( nextCouponDate ) < fnDatetoInt( dtPriceDay ) ) { prevCouponDate = nextCouponDate; nextCouponDate = fnAddDateInt( dtBaseDate, MONTH, pBondInfo->nIntMonth * nCouponIdx++ );
}
}
// 다음부터는 발행일 말일이든, 만기일 말일이든, 로직이 큰 차이는 없고 날짜만 체크하면 된다.
...
중략
...
//
/*-------------------------------------------------------------------------
* YTM / SPOT에 따른 cashflow 할인 계산 ->가격계산
*-----------------------------------------------------------------------*/
if ( pCurve->nCurveType == YTM )
{
pBondPrice->nYtm = 0.0;
if ( pCurve->nYieldCount == 1 )
{
pBondPrice->nYtm = pCurve->nYield[ 0 ];
}
else
{
/* 해당 잔존만기의 수익률을 선형보간으로 가져옴 */
UINT nRemDay;
nRemDay = pCashFactor[ nTotalCoupon - 1 ].nRemDay;
pBondPrice->nYtm = fnGetRate( pCurve, nRemDay, LINEAR );
}
idx = 0;
nextDate = nextCouponDate;
prevDate = prevCouponDate;
// 날짜를 loop 돌면서 discount factor를 구해주기 시작한다.
// discount factor란 각 이자지급일의 1원이 현재 가치로 얼마가 될 것인지 할인비율을 계산한 값이다.
while ( fnDatetoInt( nextDate ) <= fnDatetoInt( pBondInfo->dtDueDay ) )
{
pCashFactor[ idx ].nRemDay = fnCountDate( dtPriceDay, nextDate, DAY );
pCashFactor[ idx ].nCash = nInterest;
pCashFactor[ idx ].nDF = 1 / pow( 1.0 + pBondPrice->nYtm / nCouponPerYear, idx );
prevDate = nextDate;
if ( nIntPayType == MATURE_MONTH_LAST_DAY || nIntPayType == ISSUE_MONTH_LAST_DAY )
nextDate = fnSetLastDay( fnAddDateInt( dtBaseDate, MONTH, pBondInfo->nIntMonth * nCouponIdx ) );
else
nextDate = fnAddDateInt( dtBaseDate, MONTH, pBondInfo->nIntMonth * nCouponIdx );
idx++;
nCouponIdx++;
}
pCashFactor[ idx ].nRemDay = fnCountDate( dtPriceDay, pBondInfo->dtDueDay, DAY );
pCashFactor[ idx ].nCash = nInterest;
pCashFactor[ idx ].nCash = nInterest * ( fnDatetoInt( pBondInfo->dtDueDay ) - fnDatetoInt( prevDate ) ) / ( fnDatetoInt( nextDate ) - fnDatetoInt( prevDate ) );
pCashFactor[ idx ].nCash += nFace;
if ( idx > 0 )
pCashFactor[ idx ].nDF = 1.0 / ( pow( 1.0 + pBondPrice->nYtm / nCouponPerYear, idx - 1) ) ;
else
pCashFactor[ idx ].nDF = 1.0;
pCashFactor[ idx ].nDF /= ( 1.0 + pBondPrice->nYtm / nCouponPerYear * (DOUBLE)( fnDatetoInt( pBondInfo->dtDueDay ) - fnDatetoInt( prevDate ) ) / (DOUBLE)( fnDatetoInt( nextDate ) - fnDatetoInt( prevDate ) ) );
idx++;
}
else pCashFactor[ idx - 1].nCash += nFace;
nTotalCoupon = idx;
// 채권가격을 계산한다.
// 각 이자지급일의 discount factor와 이자 또는 원금을 곱해서 현재가치에 누적해서 더한다.
nBondPrice = 0.0;
nNextCouponRemDay = fnCountDate( dtPriceDay, nextCouponDate, DAY );
nCouponTermDay = fnCountDate( prevCouponDate, nextCouponDate, DAY ) ;
nDiscountToday = (DOUBLE) nNextCouponRemDay / (DOUBLE) nCouponTermDay;
for ( idx = 0; idx < nTotalCoupon; idx++ ) { if ( pCashFactor[ idx ].nRemDay == 0 ) continue; // 각 이자의 현재가치(할인금액)는 다음 이자 지급일까지의 할인율을 곱한다 nCashIn = pCashFactor[ idx ].nCash * pCashFactor[ idx ].nDF; // 다음 이자지급일까지 할인된 금액을 다시 현재까지로 할인한다. 두개의 산식을 합해서 하나로 해도 무방하다. nCashIn /= ( 1.0 + ( pBondPrice->nYtm / nCouponPerYear * nDiscountToday ) );
// 듀레이션을 같이 곱한다.
nDuration += ( nCashIn * pCashFactor[ idx ].nRemDay / 365.0 ) ;
nConvexity += ( nCashIn * pow( pCashFactor[ idx ].nRemDay/ 365.0, 2 ) * pCashFactor[ idx ].nRemDay / 365.0 );
nBondPrice += nCashIn;
}
// 듀레이션과 컨벡서티도 계산한다.
nDuration /= nBondPrice;
nMD = Math_Round( nDuration / ( 1 + pBondPrice->nYtm * pBondInfo->nIntMonth / 12.0 ), 5 );
nConvexity = Math_Round( nConvexity / ( pow( 1 + pBondPrice->nYtm * pBondInfo->nIntMonth / 12.0, 2 ) * nBondPrice ), 5 ) ;
}
// 만약 YTM이 아니라면 spot rate를 선형보간해서 해당 날짜의 할인율을 구해서 discount factor로 사용한다.
else {
...
}
// 가격과 듀레이션, 컨벡서티를 리턴한다.
pBondPrice->nPrice = nBondPrice;
pBondPrice->nDuration = Math_Round( nDuration, 5 );
pBondPrice->nMD = nMD;
pBondPrice->nConvexity = nConvexity;
free(pCashFactor);
return SUCCESS;
}
고민하지 않고 로직 구현에만 신경을 써서 작성한 코드라 표현이 거칠고 정교화되지 않은 부분이 있겠지만 전체적인 로직 이해에는 큰 무리가 없을 것 같다.
가격 계산 로직의 핵심은 각 이자지급일을 정확히 계산하는 것과 해당일의 discount factor, 즉 할인률을 계산해서 지급하는 이자 및 원금(cashflow)을 현재가치로 계산하는 것이다.
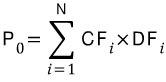
그리고 이미 설명한 바와 같이 날짜 계산 함수들이 필수이다.